「リアルタイムグラフィックスの数学」勉強ログ - 第6章 胞体ノイズ
目次
はじめに
「リアルタイムグラフィックスの数学」の第 6 章の胞体ノイズについての勉強ログです。
胞体ノイズとは?
値ノイズと勾配ノイズは格子点でのランダムな値を使ったノイズ関数でした。一方この章で学ぶ胞体ノイズは距離を使ってつくられます。胞体(セル)とは生物の細胞などのことで、胞体ノイズは「近さ」によって空間をバラバラに分割します。
第 1 近傍距離とボロノイ分割
胞体ノイズは空間内に点をバラまいて、各点への距離を測ることで得られますが、バラまかれたこれらの点は特徴点と呼ばれます。ここで特徴点をとします。空間内の点 P を定めたとき、P から特徴点への距離をで表すと、すべての特徴点までの距離の最小値は次のように求まります。
この距離の最小値のことを第 1 近傍距離と呼び、第 1 近傍距離を与える点、つまり最も近くにある特徴点を第 1 近傍点と呼びます。
特徴点の分布
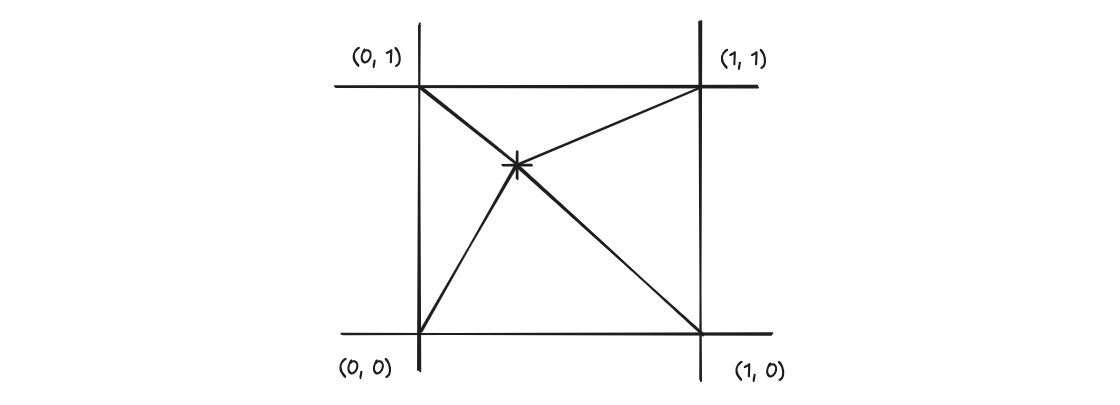
胞体ノイズは特徴点をランダムにバラまくことによって得られます。ここで特徴点のバラまき方に規則性をもたせることにします。座標が整数値であるようにすると第 1 近傍点は容易に分かります。例えば点 Pの場合は、座標が第 1 近傍点となり、第 1 近傍距離はとなります。ここで第 1 近傍距離をとる関数をとすると、になります。
次に乱数を使って特徴点をマスの内部でずらし、それを新たに特徴点としてみます。特徴点の位置ベクトルは次のように
となります。この場合、容易に第 1 近傍点を特定できないので、いくつかの候補となる特徴点への距離を計算して比べる必要があります。縦横 1 の正方形の中には必ず 1 つの特徴点が含まれるので、第 1 近傍距離は以下になります。
したがって、点 P が含まれるマスに対し、そのマスから以内の距離にある上下左右 2 つ隣までのマスをすべて探索すれば、必ず第 1 近傍点は見つけることができます。
コードで書くと次のようになります。
float fdist(vec2 p) {
vec2 n = floor(p + 0.5); // 最も近い格子点
float dist = sqrt(2.0); // 第1近傍距離の上限
for (float j = - 2.0; j <= 2.0; j++) {
for (float i = - 2.0; i < 2.0; i++) {
vec2 grid = n + vec2(i, j); // 近くの格子点
vec2 jitter = sin(u_time) * (hash22(grid) - 0.5); // 特徴点と格子点のずれ
dist = min(dist, distance(grid + jitter, p)); // 第1近傍距離を更新
}
}
return dist;
}この関数は、2 つ隣まどのマスに含まれる特徴点への距離を順に計算し、第 1 近傍距離の上限値を初期値にし、下回る場合に値を更新します。
乱数の大きさをサイン関数によって動かせば、特徴点が格子からずれるに従って、歪に動くことになります。

パフォーマンス改良
先ほどのコードは 2 つ隣までのマスを端からしらみ潰しに探索してますが、この方法ではマスの探索が必要です。探索方法を効率化して、探索対象のマスを減らしてみます。改良版のコードは次のようになります。
float fdist21(vec2 p) {
vec2 n = floor(p + 0.5); // 最も近い格子点
float dist = sqrt(2.0);
for (float j = 0.0; j <= 2.0; j++) {
vec2 grid; // 近くの格子点
grid.y = n.y + sign(mod(j, 2.0) - 0.5) * ceil(j * 0.5);
if (abs(grid.y - p.y) - 0.5 > dist) {
continue;
}
for (float i = -1.0; i <= 1.0; i++) {
grid.x = n.x + i;
vec2 jitter = hash22(grid) - 0.5;
dist = min(dist, length(grid + jitter - p));
}
}
return dist;
}まずは、y 方向(行)の探索を見てみます。
for (float j = 0.0; j <= 2.0; j++) {
vec2 grid; // チェックする格子点の座標
// Y方向に探索する範囲を決める
grid.y = n.y + sign(mod(j, 2.0) - 0.5) * ceil(j * 0.5);
// 縦方向で既に "dist" より離れていたらスキップ
if (abs(grid.y - p.y) - 0.5 > dist) {
continue;
}
}grid.yはjの値により次のようになります。
j = 0のとき、grid.y = n.yj = 1のとき、grid.y = n.y + 1.0j = 2のとき、grid.y = n.y - 1.0
近傍点は中央近くのマスにある確率が高いので、このように中心から離れるように探索するほうが効率的になります。また、改良前のコードは 2 つ隣のマスまで探索しましたが、2 つ隣のマスに第 1 近傍点が含まれるのは特殊な場合なので 1 つ隣までに制限しています。
このように中心から探索して、よりも離れていたら、その行の特徴点の計算をスキップすることができます。
for (float i = -1.0; i <= 1.0; i++) {
grid.x = n.x + i;
vec2 jitter = hash22(grid) - 0.5;
dist = min(dist, length(grid + jitter - p));
}先述とおり 1 つ隣まで探索するので、x 方向は、n.x - 1, n.x, n.x + 1を調べます。あとは同様にランダムな特徴点とpとのユークリッド距離を計算し、最短距離の場合更新します。
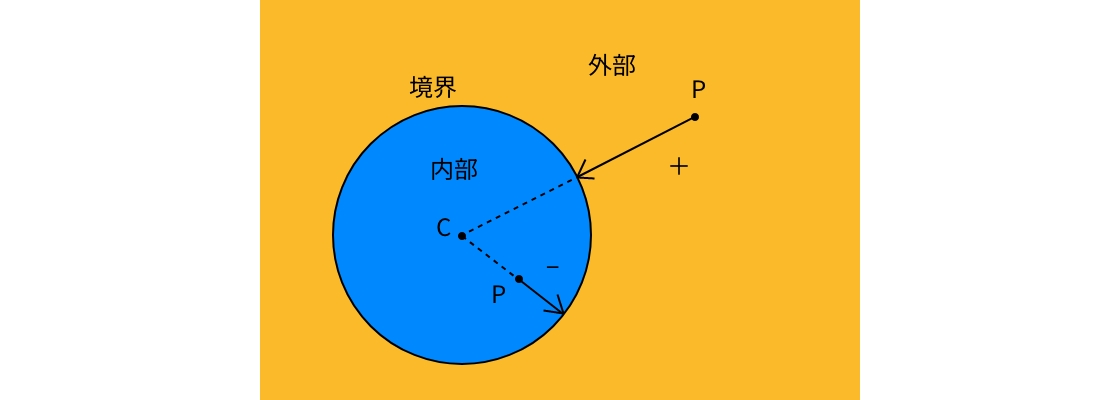
第 1 近傍距離をとる関数の勾配

第 1 近傍距離をとる関数の勾配を可視化したものが上図になります。は特徴点で値が 0 になりますが、特徴点の周りで勾配の向きも回転しています。また、特徴点と特徴点との間の境界線上で色が反転しているので、勾配の向きが切り替わっています。この境界線が次に紹介するボロノイ分割を与えます。
ボロノイ分割
ボロノイ分割とは、簡単に言えばある領土を公平に分配するための分割です。例えば、隣の集落との境界線を引くのに最も公平な方法は、隣り合う集落同士の中心点からそれぞれ線を引いて、境界線は垂直二等分線となるように線を引くことです。
次はボロノイ分割したセルの塗り分けのコードになります。
vec2 voronoi2(vec2 p) {
vec2 n = floor(p + 0.5);
float dist = sqrt(2.0);
vec2 id; // ボロノイ胞体のID変数
for (float j = 0.0; j <= 2.0; j++) {
vec2 grid;
grid.y = n.y + sign(mod(j, 2.0) - 0.5) * ceil(j * 0.5);
if (abs(grid.y - p.y) - 0.5 > dist) {
continue;
}
for (float i = -1.0; i <= 1.0; i++) {
grid.x = n.x + i;
vec2 jitter = hash22(grid) - 0.5;
// 第1近傍距離が更新される場合
if (length(grid + jitter - p) <= dist) {
dist = length(grid + jitter - p); // 距離を更新
id = grid; // IDとして格子点をとる
}
}
}
return id; // IDを返す
}先ほどのは第 1 近傍距離を返していましたが、ここでは第 1 近傍点の ID(格子点)を返すように変更し、その情報に対して色を決定するようにしてます。この ID から乱数を使って色を対応させると、モザイクタイルのようにタイル張りされます。3 変数に拡張されたを改変すれば、同様に 3 次元ボロノイ分割もつくることができます。

胞体ノイズの構成
ここまでは、1 番近い特徴点のみを計算しましたが、さらに 2 番目以降に近い特徴点の距離を計算してみましょう。i 番目に近い特徴点を第 i 近傍点、第 i 近傍点との距離を第 i 近傍距離とし、第 i 近傍距離を返す関数をとします。
次のコードはの実装(第 4 近傍距離までの探索)になります。
// 暫定4位までの値を成分するlistと値vを比較して並べ替え
vec4 sort(vec4 list, float v) {
bvec4 res = bvec4(step(v, list)); // 比較結果の真偽値
return res.x ? vec4(v, list.xyz) :
res.y ? vec4(list.x, v, list.yz) :
res.z ? vec4(list.xy, v, list.z) :
res.w ? vec4(list.xyz, v):
list;
}
vec4 fdist24(vec2 p) {
vec2 n = floor(p + 0.5);
vec4 dist4 = vec4(length(1.5 - abs(p - n))); // 第4近傍距離の上限
for (float j = 0.0; j <= 4.0; j++) {
vec2 grid;
grid.y = n.y + sign(mod(j, 2.0) - 0.5) * ceil(j * 0.5);
if (abs(grid.y - p.y) - 0.5 > dist4.w) {
continue;
}
for (float i = -2.0; i <= 2.0; i++) {
grid.x = n.x + i;
vec2 jitter = hash22(grid) - 0.5;
dist4 = sort(dist4, length(grid + jitter - p)); // 近傍距離の更新
}
}
return dist4;
}第 1~4 近傍点を見つけるには、2 つ隣のマスまでを探索します。第 1 近傍点を探索したように、第 4 近傍距離の上限値を初期値とした 4 次元ベクトルdist4を順に更新し、近傍距離を求めます。特徴点との距離を計算したら、dist4との値を比較し、値が小さい場合は更新します。

特徴点の近傍
近傍距離の意味は階段関数で二値化すると分かります。の値を二値化してみます。
void main() {
// ...
float thr = 0.7; // しきい値
bvec4 dist4b = bvec4(step(thr, fdist24(pos))); // しきい値を上回るとき真となる真偽値ベクトル
gl_FragColor = dist4b.x ? vec4(1.0, 1.0, 1.0, 1.0) : // しきい値 < F1のとき白
dist4b.y ? vec4(1.0, 0.0, 0.0, 1.0) : // F1 < しきい値 < F2のとき赤
dist4b.z ? vec4(0.0, 1.0, 0.0, 1.0) : // F2 < しきい値 < F3のとき緑
dist4b.w ? vec4(0.0, 0.0, 1.0, 1.0) : // F3 < しきい値 < F4のとき青
vec4(0.0, 0.0, 0.0, 1.0); // F4 < しきい値のとき黒
}
結果を見てみると、の値のしきい値処理が円盤の重なり方と対応します。円盤と重ならない部分は白、1 枚重なる部分は赤、2 枚重なる部分は緑、3 枚重なる部分は青、4 枚重なる部分は黒になります。つまり多く重なる部分はの値が小さくなります。
この円盤は特徴点からの距離がしきい値以内の領域を表していますが、このようなある点から一定距離以内にある領域を近傍と呼びます。
胞体ノイズ
値ノイズと勾配ノイズはサーフレットをもとにつくられていましたが、胞体ノイズはをもとにノイズをつくります。ここではに重みをつけて、総和の絶対値をとってみます。重みを変えることで、様々なテクスチャがあらわれます。
vec4 wt; // 重み
float cnoise21(vec2 p) {
return abs(dot(wt, fdist24(p)));
}
次回リンク
後で詳しく調べるものリスト
- ボロノイ分割の境界線を描く
https://iquilezles.org/articles/voronoilines/ - ボロノイ分割の平滑化
https://iquilezles.org/articles/smoothvoronoi/
https://iquilezles.org/articles/voronoise/