「リアルタイムグラフィックスの数学」勉強ログ - 第5章ノイズの調理法
目次
はじめに
「リアルタイムグラフィックスの数学」の第 5 章のノイズの調理法についての勉強ログです。
再帰
再帰関数とは、関数の中で自分自身の関数を呼び出すような関数のことです。GLSL では再帰関数は使えませんが、for 文を使って再帰的な処理を行うことができます。
非整数ブラウン運動(fBM)
1 以下の定数 G に対し、1 変数ノイズ関数 noise(x)の周波数を 2 倍するごとに値を G 倍して、それを足し合わせてみましょう。式にすると次のようになります。
ここで素材となるノイズ関数 noise(x)はどのような関数でもいいですが、値の範囲を区画にずらしておきます。このように加工されたノイズ関数は非整数ブラウン運動(fractional Brownian motion, fBM)と呼ばれます。
ノイズ関数として値ノイズを使用した fBM のコードは次のようになります。
float fbm21(vec2 p, float g) {
float val = 0.0; // 値の初期値
float amp = 1.0; // 振幅の重みの初期値
float freq = 1.0; // 周波数の重みの初期値
for (int i = 0; i < 4; i++) {
val += amp * (vnoise21(freq * p) - 0.5); // [-0.5, 0.5]区画にずらす
amp *= g; // 繰り返しのたびに振幅をg倍
freq *= 2.01; // 繰り返しのたびに周波数を倍増
}
return 0.5 * val + 0.5; // 値の範囲を[0, 1]区画に正規化
}式では周波数を 2 倍していましたが、格子由来のクセがあらわれるのを防ぐために、周波数の倍数をぴったりの 2.0 ではなく少しずらした 2.01 を使用します。
下図は、上が値ノイズで下がパーリンノイズを素材にした fBM の結果になります。

G の値が 0 から 1 に近づくにしたがって、ノイズの粗さが変化することが分かります。fBM は繰り返し操作を行うため処理が重くなりがちなため、軽くする場合は値ノイズを使うことが好まれます。
ドメインワーピング
ノイズ関数の値に再帰的な処理を加えたものが fBM でしたが、値ではなく座標に再帰的な処理を加えたものはドメインワーピングと呼ばれます。
定数 G を用意し、新たなノイズ関数を次のようにつくります。
これはノイズのテクスチャ座標を、G だけ重みをつけたノイズ関数で歪ませています。これを繰り返すと次のようになります。
値ノイズを素材にした fBM を使用したドメインワーピングのコードは次のようになります。
float warp21(vec2 p, float g) {
float val = 0.0;
for (int i = 0; i < 4; i++) {
val = fbm21(p + g * val, 0.5);
}
return val;
}下図は、上が fBM、下がパーリンノイズを素材にしたドメインワーピングの結果になります。

座標にノイズ関数の値を加えることで歪めていますが、歪める方向が常に同じ方向になるので、歪ませる方向のクセがついてしまいます。これを防ぐために、ノイズ関数の値を回転のパラメータに使うことで、歪ませる方向をずらすことができます。
ここでは、vec2(cos(2.0 * PI * val), sin(2.0 * PI * val))を G かけることで、歪ませる方向をずらすことができます。
float warp21(vec2 p, float g) {
float val = 0.0;
for (int i = 0; i < 4; i++) {
val = fbm21(p + g * vec2(cos(2.0 * PI * val), sin(2.0 * PI * val)), 0.5);
}
return val;
}結果は下図のようになります。

階調の変換
フラグメントシェーダでは最終的に fragColor 変数に代入された値によって、各ピクセルの色が決まります。fragColor 変数に値を代入する前に最終段階で別の関数を合成すると、色の濃度の対応付けを変化させることができます。この関数を階調変換関数と呼びます。また、そのグラフのことをトーンカーブと呼びます。
以下は階調変換関数で変更する前の、fBM を使用したドメインワーピングの元画像になります。

二階調化

二階調化はある範囲を基準に 0 か 1 かの値に変換します。これは GLSL ではstep関数を使用することで実現できます。デモでは時間によって範囲を変更しています。
float converter(float v) {
float time = abs(mod(0.1 * u_time, 2.0) - 1.0);
return step(time, v);
}ポスタリゼーション

ポスタリゼーションは第 1 章でみたように、出力値が階段状で変化します。サンプルコードでは時間によって数段階変化し最大が 8 段階になります。
float converter(float v) {
float time = abs(mod(0.1 * u_time, 2.0) - 1.0);
float n = floor(8.0 * time);
return (floor(n * v) + step(0.5, fract(n * v))) / n;
}S 字トーンカーブ

S 字トーンカーブは、S 字型のトーンカーブを利用した変換をします。これは画像のコントラストが上がったような効果をもたらします。S 字型にするためにはsmoothstep関数を使用します。
float converter(float v) {
float time = abs(mod(0.1 * u_time, 2.0) - 1.0);
return smoothstep(0.5 * (1.0 - time), 0.5 * (1.0 + time), v);
}ガンマ補正

ガンマ補正は、pow(x, a)によってを計算します。トーンカーブは のとき上に膨らんだ曲線になり画像の明るさは増します。逆に のときは下に膨らんだ曲線になり全体的に明るさは落ちます。このようにべき乗を使った明るさ調整をガンマ補正と呼びます。
float converter(float v) {
float time = abs(mod(0.1 * u_time, 2.0) - 1.0);
return pow(v, time);
}ソラリゼーション

ソラリゼーションはサイン波のようなトーンカーブを使用します。これは画像の濃淡の一部分を反転させることにより、ネガ画像とポジ画像が混ざりあったような効果が得られます。
float converter(float v) {
return 0.5 * sin(4.0 * PI * v + u_time) + 0.5;
}それぞれのデモの画像処理に関して詳しく知りたい方は下記の書籍をおすすめします。
ブレンディング
複数の画像からその中間の画像をつくることをブレンディングと呼びます。GLSL ではmix関数を使用することで 2 つの画像をブレンディングすることができます。サンプルコードは次のようになります。
vec3 blend(float a, float b) {
float time = abs(mod(0.1 * u_time, 2.0) - 1.0);
vec3[2] col2 = vec3[](
vec3(a, a, 1.0), // aの値を青と白の中間色に変換
vec3(0.0, b, b) // bの値を黒と緑の中間色に変換
);
return mix(
col2[0],
col2[1],
smoothstep(0.5 - 0.5 * time, 0.5 + 0.5 * time, b / (a + b))
);
}
void main() {
vec2 pos = gl_FragCoord.xy / min(u_resolution.x, u_resolution.y);
pos = 10.0 * pos + u_time;
float a = warp21(pos, 1.0);
float b = warp21(pos + 10.0, 1.0);
vec3 col = blend(a, b);
fragColor = vec4(col, 1.0);
}ここでは、ドメインワーピングを使用した素材を 2 つ用意してます。1 つは 10.0 ずらしておきます。
blend関数をみてみると、col2[0]には a の値を青と白の中間色に変換した結果が入っており、col2[1]には b の値を黒と緑の中間色に変換した結果が入っています。これをmix関数で補間します。また、mix関数の第 3 引数では、a と b の値の比に応じて補間しており、a の比重が大きいほどcol2[0]の色が強く出ます。

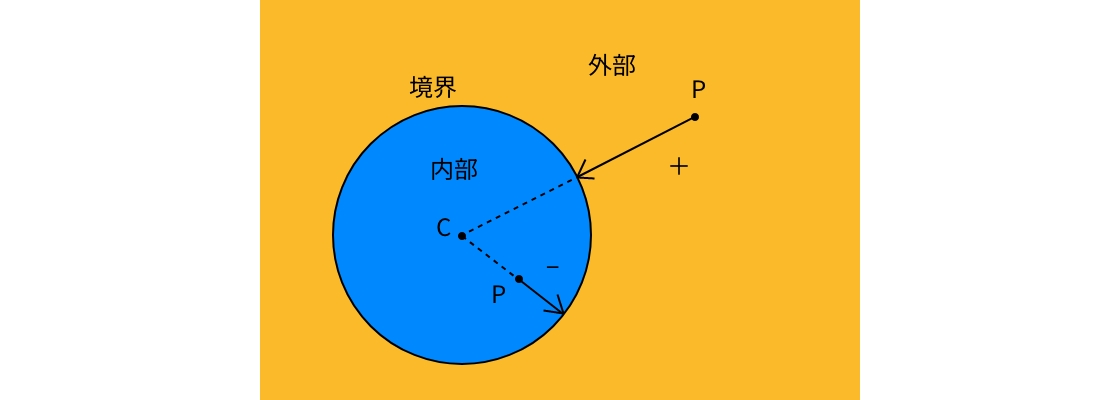
集合演算
与えられた集合に対し、その和集合や補集合、共通部分をとる操作を**集合演算(ブーリアン演算)**と呼びます。集合演算は下図に示すベン図と呼ばれる模式図によって表すことができます。

画像を二値化すると値が 0 か 1 の部分に分けられます。真偽値と論理演算を使うことによって、2 つの二値画像の集合演算ができます。コードで書くと次のようになります。
vec2 f = vec2(warp21(pos, 1.0), warp21(pos + 10.0, 1.0));
f -= 0.5; // 値を[-0.5, 0.5]にずらす
vec4 x;
bvec2 b = bvec2(step(f, vec2(0))); // 0より小さければ真、そうでなければ偽
x = vec4(
b[0] && b[1], // 共通部分
b[0] && !b[1], // 差集合
!b[0] && b[1], // 差集合
!(b[0] || b[1]) // 和集合の補集合
);
vec3[4] col4 = vec3[](
vec3(1.0, 0.0, 0.0), // 赤
vec3(0.0, 1.0, 0.0), // 緑
vec3(0.0, 0.0, 1.0), // 青
vec3(1.0, 1.0, 0.0) // 黄
);
for (int i = 0; i < 4; i++) {
fragColor.rgb += x[i] * col4[i];
}bvec2 bはstep関数によって 0 と 1 に分け、それを真偽値に型変換しています。ここで 0 は偽(false)、1 は真(true)となります。
xでは真偽値に対する論理演算を行っています。論理積&&は共通部分に、論理和||は和集合に、論理否定!は補集合に該当します。この論理演算を行った真偽値を 0 と 1 の数値に戻して、それに色を対応させて塗り分けています。
色の塗り分けは、上記のベン図と同様に、共通部分は赤、差集合はそれぞれ青と緑、和集合の補集合は黄色に塗り分けます。fBM とパーリンノイズのドメインワーピングに対して上記の集合演算をした結果が下図になります。

次回リンク
後で詳しく調べるものリスト
-
ドメインワーピング
https://iquilezles.org/articles/warp/ -
画像処理の数学
-
max と min による集合演算

![ディジタル画像処理[改訂第二版]](https://m.media-amazon.com/images/I/51nkfyU1a-L._SY522_.jpg)