「リアルタイムグラフィックスの数学」勉強ログ - 第1章補間
目次
はじめに
「リアルタイムグラフィックスの数学」の第 1 章の補間についての勉強ログです。
線形補間とグラデーション
mix 関数について
GLSL における mix 関数は以下のような数式になります。
これは、線分 AB があり、その線分上を動く 0 以上 1 以下の x に対して、線分 AB を x: (1 - x)に内分する点の位置ベクトルを表しています。上記の式のベクトルをmix(a, b, x)として定義しています。このように 2 点間をつなぐことを補間と呼び、上記の式は線形補間(Linear Interpolation)の公式です。
コード 1.1 のように、赤(1, 0, 0)と青(0, 0, 1)を mix 関数でつなぐことで 2 色のグラデーションを作ることができます。
vec2 RED = vec3(1.0, 0.0, 0.0);
vec3 BLUE = vec3(0.0, 0.0, 1.0);
vec3 col = mix(RED, BLUE, pos.x);
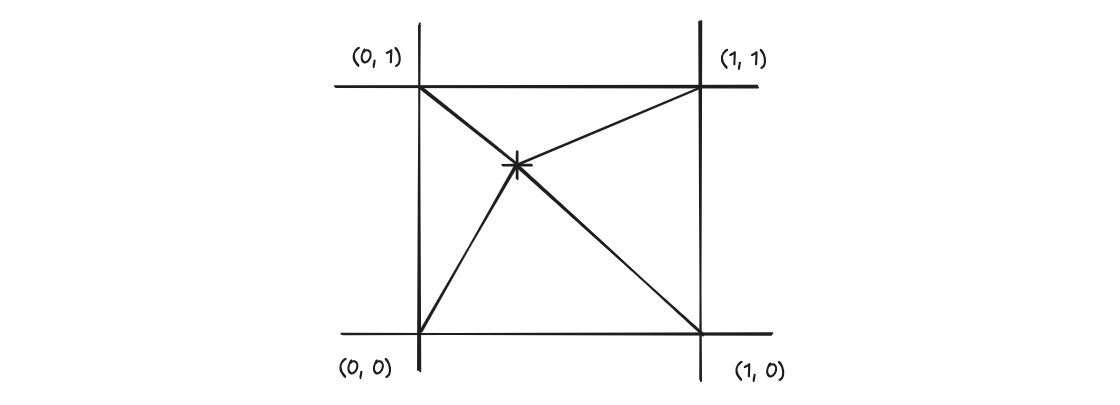
双線形補間
補間関数を 2 変数にすると、2 次元区間上の補間を考えることができる。下記の 2 変数関数を考える。
と に と を代入するとそれぞれ、、、、になるのを確認してみてください。
コード 1.3 では、4 色をつなぐグラデーションを作成してます。

が赤で、が青、が緑で、が黄色となり、その間はグラデーションになっているのが確認できるでしょう。
階段関数によるポスタリゼーション
線形補間は連続的につなぐ補間ですが、ポスタリゼーションは離散的な値で補間を行う方法です。コード 1.4 では、step 関数と fract 関数,floor 関数を用いてポスタリゼーションを実装してます。
次のコード 1.4 では、双線形補間でが赤で、がピンク、が黄色で、が白となるグラデーションを作成し、ポスタリゼーションで階段状に補間しています。

void main(){
vec2 pos = gl_FragCoord.xy / u_resolution.xy;
vec3[4] col4 = vec3[](
vec3(1.0, 0.0, 0.0),
vec3(1.0, 1.0, 0.0),
vec3(1.0, 0.0, 1.0),
vec3(1.0, 1.0, 1.0)
);
float n = 4.0;
pos *= n;
pos = floor(pos) + step(0.5, fract(pos));
pos /= n;
vec3 col = mix(mix(col4[0], col4[1], pos.x), mix(col4[2], col4[3], pos.x), pos.y);
fragColor = vec4(col, 1.0);
}ここで階段状に補間してる部分の数式を床関数を[]で表すと以下のようになってます。
サンプルコードでは フラグメント座標範囲を[0, 4]にスケールし、4 分割しています。
ここで、Desmos 上で先程のポスタリゼーションの数式を見てみましょう。分かりやすいように 5 分割にしています。

になるので、y 軸方向では 0.2 ずつ増加してるのが分かるかと思います。x 軸方向も同様に 0.2 ずつ増加していますが、[0.0, 0.1]と[0.9, 1.0]の範囲は 0.1 の増加になります。
なので、先程のサンプルコードの画像も両端は半分の区切りになります。実際に値を代入してみて、グラフ通りになるか確認してみてください。
極座標を使ったマッピング
極座標について
直交座標(デカルト座標)では点をの形で表しますが、極座標では、点を距離と角度を使って表します。極座標では次のようになります。
- : 原点からの距離(動径)
- : x 軸正方向からの角度(偏角)
極座標と直交座標の変換は以下のようになります。
GLSL では、動径は組み込み関数のlengthで計算できます。偏角の arctan はatanで計算できますが、上では定義されてないので、拡張したatan2関数を作ります。
const float PI = 3.1415926;
float atan2(float y, float x) {
return x == 0.0 ? sign(y) * PI / 2.0 : atan(y, x);
}sign関数は、値が正なら 1、負なら-1、 なら を返します。ここでは、 の場合なので、y が正ならになり 90 度、負ならになり-90 度となることを表してます。
このatan2関数を使用し、直交座標を極座標に変換するxy2pol関数は次のようになります。
vec2 xy2pol(vec2 xy) {
return vec2(atan2(xy.y, xy.x), length(xy));
}極座標を直交座標に変換するpol2xy関数は次のようになります。
vec2 pol2xy(vec2 pol) {
return pol.y * vec2(cos(pol.x), sin(pol.x));
}引数のpolは、極座標の形で表されます。pol.xは偏角、pol.yは動径です。
マッピング
ここでは、サンプルコード 1.2 の直交座標での 3 色(赤・青・緑)をつなぐグラデーションを極座標にマッピングしてみます。

// 0~2πの範囲で返す関数
float atan2PI(float y, float x) {
float a = atan2(y, x);
return (a < 0.0) ? a + 2.0 * PI : a;
}
void main(){
vec2 pos = gl_FragCoord.xy / u_resolution.xy;
pos = 2.0 * pos.xy - vec2(1.0);
pos.x = atan2PI(pos.y, pos.x) / PI;
vec3[3] col3 = vec3[](
vec3(1.0, 0.0, 0.0),
vec3(0.0, 0.0, 1.0),
vec3(0.0, 1.0, 0.0)
);
int ind = int(pos.x);
vec3 col = mix(col3[ind], col3[ind + 1], fract(pos.x));
fragColor = vec4(col, 1.0);
}まず極座標にマッピングするため、画面中央が(0.0, 0.0)になるように、フラグメント座標範囲を[-1.0, 1.0]に変換します。
vec2 pos = gl_FragCoord.xy / u_resolution.xy;
pos = 2.0 * pos.xy - vec2(1.0); // [-1.0, 1.0] に変換GLSL のatanは、[-π,π] の範囲を返すので、3 色のグラデーションにするために、偏角を [0,2π] の範囲で返す関数atan2PIを作ります。
float atan2PI(float y, float x) {
float a = atan2(y, x);
return (a < 0.0) ? a + 2.0 * PI : a;
}GLSL のatanは、座標の第 1 象限と第 2 象限の場合は正の値、第 3 象限と第 4 象限の場合は負の値を返します。なので、正の値の時はそのまま返して、負の値の時は 2π を加えて返すことで、[0,2π] の範囲で返すことができます。
atan2PIで返ってきた値を π で割ることで、0~2 の範囲が得られるので、サンプルコード 1.2 のようにintで整数にして、3 色の配列のインデックスを使いmix関数でグラデーションを作ることができます。
ここで見たように、極座標を使ったマッピングでは原点に近い部分では、1 周が短くなります

なので書籍のコード 1.8 では、テクスチャの端でつなぎ目がうまくつながるように白色のグラデーションをつくっています。この部分に関しては書籍を参照してください。
次回リンク
後で詳しく調べるものリスト
-
バイリニア補間、双線形補間
 バイリニア補間
バイリニア補間数学において、バイリニア補間 とは、反復線形補間を用いて2変数(例えばxとy)の関数を補間する方法である。 通常は2次元の不規則格子 上でサンプリングされた関数に適用されるが、任意の凸四辺形(のポリゴンメッシュ)の頂点上に定義された関数にも一般化できる。
Wikipedia -
ポスタリゼーションによる画像処理
 Posterization
PosterizationPosterization or posterisation of an image is the conversion of a continuous gradation of tone to several regions of fewer tones, causing abrupt changes from one tone to another. This was originally done with photographic processes to create posters. It can now be done photographically or with digital image processing, and may be deliberate or an unintended artifact of color quantization. Posterization is often the first step in vectorization (tracing) of an image.
Wikipedia -
smoothstep の数式の導入方法
-
HSV 色空間
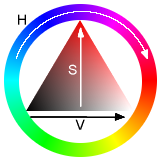 HSV色空間
HSV色空間HSV色空間 は色相 (Hue)、彩度 、明度 の三つの成分からなる色空間。HSBモデル とも言われる。
Wikipedia