「リアルタイムグラフィックスの数学」勉強ログ - 第4章勾配ノイズ

◯目次

はじめに
勾配ノイズとは？
勾配ノイズの構成法
- 1 変数
- 2 変数
値ノイズと勾配ノイズの違い
勾配の回転
パーリンノイズ
- 2 次元のパーリンノイズ
次回リンク
後で詳しく調べるものリスト
参考書籍

はじめに
勾配ノイズとは？
勾配ノイズの構成法
- 1 変数
- 2 変数
値ノイズと勾配ノイズの違い
勾配の回転
パーリンノイズ
- 2 次元のパーリンノイズ
次回リンク
後で詳しく調べるものリスト
参考書籍

はじめに#

「リアルタイムグラフィックスの数学」の第 4 章の勾配ノイズについての勉強ログです。

リアルタイムグラフィックスの数学 ― GLSLではじめるシェーダプログラミング巴山竜来 Amazon.co.jpで購入する

勾配ノイズとは？#

前回は値ノイズについて見てきました。値ノイズは計算量も少なく、簡単につくれるノイズですが、格子で区切っているのでブロック状に見えてしまいますし、ムラが現れやすいです。値ノイズを改善したノイズが勾配ノイズになります。

値ノイズの場合は、格子点での乱数の「値」を使うのに対し、勾配ノイズは乱数のベクトル値を「勾配」として使用します。ノイズ関数でよく使用されるパーリンノイズは、この勾配ノイズの一種であります。この章では、勾配ノイズと 2002 年の Perlin による改良版勾配ノイズ（パーリンノイズ）について見ていきます。

勾配ノイズの構成法#

1 変数#

値ノイズは乱数値をエルミート補間してつくりました。ここで別の見方として、 $h(0) = 0$ , $h(1) = 1$ , $h'(0) = h'(1) = 0$ を満たすエルミート補間関数 $h(x)$ に対して、 $w(x)$ を次のように定義します。

w(x) = \begin{cases} h(x + 1) & (-1 \le x \lt 0) \\ 1 - h(x) & (0 \le x \lt 1) \\ 0 & (x \lt -1, 1 \le x) \end{cases}

この関数は下図のように原点で最大値 1 をとり、 $[-1, 1]$ 区画外では値 0 となります。このような特定の区画以外では 0 となる関数は窓関数と呼びます。

値ノイズはこの窓関数の和で表すことができます。1 変数の場合に、例えば $x = -1, 0, 1$ に対応する乱数値が 0.3,0.9,0.6 ならば、 $[-1, 1]$ 区間上で値ノイズ $vnoise(x)$ は次のようになります。

vnoise(x) = \begin{cases} \mathrm{mix}(0.3, 0.9, h(x + 1)) = 0.3w(x + 1) + 0.9w(x) & (-1 \le x \le 0)\\ \mathrm{mix}(0.9, 0.6, h(x)) = 0.9w(x) + 0.6w(x - 1) & (0 \le x \le 1) \end{cases}\\ \tag{4.1} = 0.3w(x + 1) + 0.9w(x) + 0.6w(x - 1)

一般に格子点 $i$ に乱数値 $v_i$ が対応していれば、値ノイズ関数は次のように与えられます。

vnoise(x) = \sum_{i} v_i w(x - i)

ここで窓関数の係数を 1 次関数に置き換えたものが勾配ノイズ関数になります。窓関数に 1 次関数をかけると、下図の青のグラフのように 1 回上下にうねるような波ができます。

この波を足し合わせることで勾配ノイズを定義します。例えば、式 $(4.0)$ の係数 0.3,0.9,0.6 を 1 次関数 $0.3(x + 1)$ , $0.9x$ , $0.6(x - 1)$ に置き換えた勾配ノイズ関数は次のように書けます。

gnoise(x) = 0.3(x + 1)w(x + 1) + 0.9xw(x) + 0.6(x - 1)w(x - 1)

この関数は、 $w(x)$ の性質より $x = -1, 0, 1$ での値は 0 になり、傾きは 0.3, 0.9, 0.6 となります。このことより勾配ノイズ関数は、格子点上に与えられた傾きにフィットするように補間する関数です。また、格子点 $i$ に乱数値 $v_i$ が対応していれば、勾配ノイズ関数は次のように与えられます。

gnoise(x) = \sum_{i} v_i (x - i)w(x - i)

2 変数#

1 変数の場合を多変数に拡張するには、窓関数を多変数にし、傾きを勾配に置き換えます。2 変数窓関数は $w(x, y) = w(x)w(y)$ となり、原点で最大値 1 をとり、領域 $(1 - |x|)(1 - |y|) \gt 0$ 外では 0 になります。

ベクトル $\boldsymbol{g} = (a, b)$ に対し、1 次関数 $ax + by = \boldsymbol{g} \cdot (x, y)$ をとると、 $\boldsymbol{g} \cdot (x, y)w(x, y)$ は原点で値が 0 になり、勾配が $\boldsymbol{g}$ となる 2 変数関数になります。これは勾配の向きに 1 回上下にうねるような波であり、サーフレットとも呼ばれます。

勾配ノイズ関数は各格子点から乱数ベクトルを取得し、各格子点ごとにそれを勾配とするサーフレットをつくって、その総和をとったものになります。各格子点 $(i, j)$ に乱数ベクトル $\boldsymbol{g}_{ij}$ が対応しているとき

gnoise(\boldsymbol{x}) = \sum_{i, j} \boldsymbol{g}_{ij} \cdot (\boldsymbol{x} - (i, j))w(\boldsymbol{x} - (i, j))

によって $\boldsymbol{x}$ での勾配ノイズの値を定義します。

$\boldsymbol{x}$ を取り囲む 4 つの格子点を、 $e_{00}, e_{10}, e_{01}, e_{11}$ とし、これらの格子点に対応する 2 次元乱数ベクトルを $\boldsymbol{g}_{00}, \boldsymbol{g}_{10}, \boldsymbol{g}_{01}, \boldsymbol{g}_{11}$ とすると、 $\boldsymbol{x}$ での勾配ノイズの値は次で与えられます。

gnoise(\boldsymbol{x}) = \sum_{i = 0}^1 \sum_{j = 0}^1 \boldsymbol{g}_{ij} \cdot (\boldsymbol{x} - e_{ij})w(\boldsymbol{x} - e_{ij})

ここで $v_{ij} = \boldsymbol{g}_{ij} \cdot (\boldsymbol{x} - e_{ij})$ , $(f_0, f_1) = \mathrm{fract}(x)$ とすると次のようなエルミート補間の形に置き換えられます。

gnoise(\boldsymbol{x}) = \mathrm{mix}(\mathrm{mix}(v_{00}, v_{10}, h(f_0)), \mathrm{mix}(v_{01}, v_{11}, h(f_0)), h(f_1))

サンプルコード 4.1 では上記の式を用いて、勾配ノイズを生成しています。

float gnoise21(vec2 p){
  vec2 n = floor(p);
  vec2 f = fract(p);
  float[4] v;
  for (int j = 0; j < 2; j ++){
    for (int i = 0; i < 2; i++){
      vec2 g = normalize(hash22(n + vec2(i,j)) - vec2(0.5)); //乱数ベクトルを正規化
      v[i+2*j] = dot(g, f - vec2(i, j)); //窓関数の係数
    }
  }
  f = f * f * f * (10.0 - 15.0 * f + 6.0 * f * f);
  return 0.5 * mix(mix(v[0], v[1], f[0]), mix(v[2], v[3], f[0]), f[1]) + 0.5;
}

処理を順を追って解説します。

勾配ベクトルの生成#

次のコードは、乱数ベクトルを正規化し勾配ベクトルを生成しています。

vec2 g = normalize(hash22(n + vec2(i,j)) - vec2(0.5));

$[0, 1]$ 範囲の乱数ベクトルをvec2(0.5)で引くことで、 $[-0.5, 0.5]$ 範囲の乱数ベクトルに変換します。これをnormalize関数を使って勾配の大きさが 1 になるように正規化し、勾配ベクトルが生成されます。各格子点ごとにランダムな方向ベクトルを生成しています。

内積の計算#

次のコードは、内積を計算しています。

v[i+2*j] = dot(g, f - vec2(i, j));

f - vec2(i, j)はサンプル点から格子点へのベクトルになります。先ほどの勾配ベクトルと内積を取ることでこの $v_{ij}$ が窓関数の係数になります。

補間#

最後に補間を取って返します。

f = f * f * f * (10.0 - 15.0 * f + 6.0 * f * f);
return 0.5 * mix(mix(v[0], v[1], f[0]), mix(v[2], v[3], f[0]), f[1]) + 0.5;

* 0.5 + 0.5の計算は、値の範囲を $[-1, 1]$ から $[0, 1]$ に収まるように正規化しています。
勾配ノイズの結果は下記のようになります。

値ノイズと勾配ノイズの違い#

値ノイズと勾配ノイズの違いは、値の分布に違いがあります。下記は値の分布を HSV 色空間で表示して可視化し、両者の値のばらつき方を比較しています。

fragColor.rgb = hsv2rgb(vec3(v, 1.0, 1.0));

値ノイズと勾配ノイズの値を HSV 色空間の色相に対応させているので、値が 0 または 1 に近い場合に赤色に近づきます。上図でみるように値ノイズの方が所々に赤い箇所があらわれていますが、勾配ノイズの場合はおおよそ青から緑色になっていますので、値が $0.5\pm0.35$ の範囲に収まっています。

実際に勾配ノイズでは格子点で必ず 0.5 の値をとるため、値ノイズと異なり値の分布は 0.5 周辺の頻度が高いことが分かります。

勾配の回転#

勾配の向きを回転させることで、勾配ノイズに動きをもたせることができます。
2 次元ベクトル $(x, y)$ は動径 $r$ と偏角 $\theta$ を使って $(r \cos \theta, r \sin \theta)$ と表すことができます。このとき加法定理を使うと次式になります。

r \cos(\theta + \theta') = r \cos \theta \cos \theta' - r \sin \theta \sin \theta' \\ r \sin(\theta + \theta') = r \sin \theta \cos \theta' + r \cos \theta \sin \theta'

よって $(x, y) = (r \cos \theta, r \sin \theta)$ を代入すると、 $(x, y)$ を $\theta'$ 回転したベクトルは次のようになります。

(x \cos \theta' - y \sin \theta', x \sin \theta' + y \cos \theta')

これをコードで実装したものがサンプルコード 4.3 になります。

2次元平面上の回転

vec2 rot2(vec2 p, float t) {
  return vec2(cos(t) * p.x - sin(t) * p.y, sin(t) * p.x + cos(t) * p.y);
}

パーリンノイズ#

勾配ノイズの問題点は、勾配のとり方によってはアーティファクトが生じることです。Perlin は 2002 年の論文で勾配ノイズの改良案を提案し、この論文にちなんだノイズはパーリンノイズと呼ばれています。

パーリンノイズでは勾配の方向を限定することで、勾配ノイズの問題点を解決しています。この改良により、アーティファクトを生じさせず、計算コストを下げる効果をもたらしています。

2 次元のパーリンノイズ#

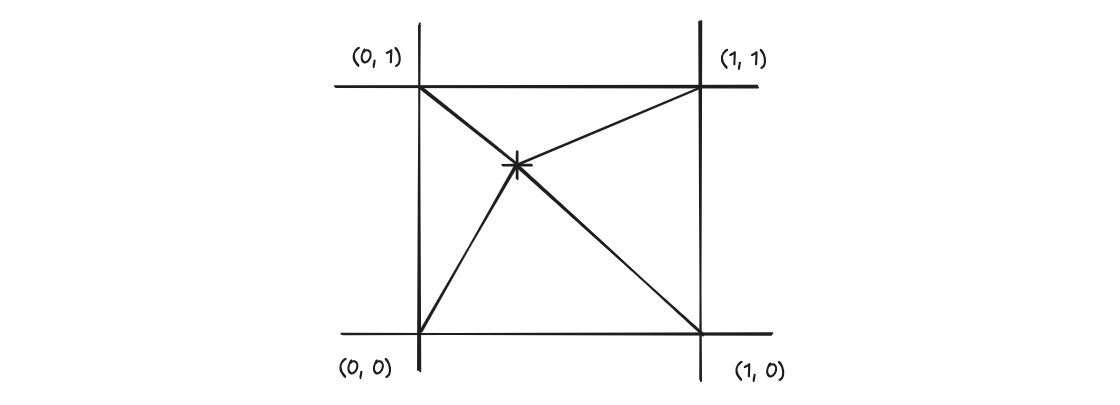
ここでは 2 次元のパーリンノイズについて説明します。勾配ノイズでは対角線方向と軸方向に勾配をとったさいにアーティファクトが生じていました。そこで図のように対角線方向と軸方向を避けて勾配を選びます。

対角線方向の角度は $\pi / 4$ の倍数なので、それを避けた角度は $n\pi / 4 + \pi / 8 (0 \le n \lt 8)$ のベクトルをとります。上図の赤線は、これらのベクトルを示しています。

上図のように 2 次元の場合は、8 個の勾配をとり $c = cos(\pi / 8), s = sin(\pi / 8)$ とすると次のようになります。

cx + sy, -cx + sy, cx - sy, -cx - sy \\ sx + cy, -sx + cy, sx - cy, -sx - cy

ここで 8 個の勾配はすべて成分が $\pm1$ か $0$ なので、その内積は成分のたし算、引き算で実装できることになります。実装では、ハッシュ値をこの 8 通りの計算に対応させることにより、勾配ノイズの計算を簡略化させています。

2 次元のパーリンノイズのコードは次のようになります。

2次元のパーリンノイズ

float gtable2(vec2 lattice, vec2 p) {
  uvec2 n = floatBitsToUint(lattice);
  uint ind = uhash22(n).x >> 29;
  float u = 0.92387953 * (ind < 4u ? p.x : p.y); // 0.92387953 = cos(pi/8)
  float v = 0.38268343 * (ind < 4u ? p.y : p.x); // 0.38268343 = sin(pi/8)
  return ((ind & 1u) == 0u ? u : -u) + ((ind & 2u) == 0u? v : -v);
}
 
float pnoise21(vec2 p) {
  vec2 n = floor(p);
  vec2 f = fract(p);
  float[4] v;
  for (int j = 0; j < 2; j++) {
    for (int i = 0; i < 2; i++) {
      v[i + 2 * j] = gtable2(n +vec2(i, j), f - vec2(i, j));
    }
  }
  f = f * f * f * (10.0 - 15.0 * f + 6.0 * f * f);
  return 0.5 * mix(mix(v[0], v[1], f[0]), mix(v[2], v[3], f[0]), f[1]) + 0.5;
}

gtable2関数では、格子点を 8 通りの計算にランダムに対応させる関数です。ハッシュ値をシフトして 2 進数の $3(=32 - 29)$ 桁、つまり 10 進数での 8 までの値に変換しています。

三項演算子を使用することで上記内積の値の計算に対応させています。

次回リンク#

後で詳しく調べるものリスト#

サーフレット
シンプレックスノイズ
この章の 2002 年の Perlin の論文
https://mrl.cs.nyu.edu/~perlin/paper445.pdf

参考書籍#

リアルタイムグラフィックスの数学 ― GLSLではじめるシェーダプログラミング巴山竜来 Amazon.co.jpで購入する

Meta Data

公開日:2025-09-20

Tags:

#GLSL #数学 #勉強ログ

image

$「リアルタイムグラフィックスの数学」勉強ログ - 第4章勾配ノイズ$

17の平面繰り返しパターンをGLSLで実装してみる - その1

はじめに

平面の繰り返しパターンは17種に分類することが、数学的に証明されています。それも4つの基本移動(並進・鏡映・回転・映進)の組み合わせで17パターンを作成できます。

詳しくは以下のWikipediaのリンクと参考書籍を参照ください。

このシリーズでは、GLSLで17の平面繰り返しパターンを実装してみます。紹介するパターンはp1~pmgまでの9パターンになります。残りのパターンは次回に紹介します。

基本的なコードの説明

このシリーズでは、対称性が分かりやすいように三角形を4つの基本移動をさせることでパターンを作成します。まずは基本的なmainのコードを説明します。

はじめに#

勾配ノイズとは？#

勾配ノイズの構成法#

1 変数#

2 変数#

勾配ベクトルの生成#

内積の計算#

補間#

値ノイズと勾配ノイズの違い#

勾配の回転#

パーリンノイズ#

2 次元のパーリンノイズ#

次回リンク#

後で詳しく調べるものリスト#

参考書籍#

はじめに

基本的なコードの説明

はじめに

3x3 行列(Mat3)

はじめに

テクスチャマッピング

はじめに

2 次元 SDF

円の SDF

はじめに

胞体ノイズとは？

第 1 近傍距離とボロノイ分割

はじめに

再帰

非整数ブラウン運動(fBM)

はじめに

値ノイズの構成法

はじめに

レガシー乱数

はじめに

線形補間とグラデーション

mix 関数について

はじめに

勉強方法の方針

Profile

Social

My Favorite

音楽