「リアルタイムグラフィックスの数学」勉強ログ - 第8章 3Dレンダリング
はじめに
「リアルタイムグラフィックスの数学」の第 8 章の 3D レンダリングについての勉強ログです。
テクスチャマッピング
地面とレイの交点を計算し、地面に市松模様をテクスチャとしてマッピングします。市松模様のテクスチャは次のようになります。
float text(vec2 st) {
return mod(floor(st.s) + floor(st.t), 2.0);
}ここで 3D 空間のカメラの設定をします。カメラの向きをとし、カメラの上方向をとします。この値に対して外積をとることで、撮影する向きに対する水平方向を得ることができます。実際の計算は次のようになります。
これらの情報を用いることで、カメラからスクリーンまでのベクトルを計算することができます。
vec3 cPos = vec3(0.0, 0.0, 0.0); // 配置位置
vec3 cDir = vec3(0.0, 0.0, -1.0); // カメラの向き
vec3 cUp = vec3(0.0, 1.0, 0.0); // カメラの上方向
vec3 cSide = cross(cDir, cUp); // 外積(カメラの水平方向)
float targetDepth = 1.0; // スクリーンまでの距離
vec3 ray = cSide * pos.x + cUp * pos.y + cDir * targetDepth; // レイの方向サンプルコードでは、マウスの y 座標によってカメラの向きを x 軸を中心に回転させ、マウスの x 座標によってカメラと地面の距離を変更します。
void main() {
vec2 p = (gl_FragCoord.xy * 2.0 - u_resolution) / min(u_resolution.x, u_resolution.y);
vec3 cPos = vec3(0.0, 0.0, 0.0);
float t = -0.5 * PI * (u_mouse.y / u_resolution.y); // マウスのy座標を回転角に対応
vec3 cDir = rotX(vec3(0.0, 0.0, - 1.0), t); // カメラの向きをx軸を中心に回転
vec3 cUp = rotX(vec3(0.0, 1.0, 0.0), t); // カメラの上方向をx軸を中心に回転
vec3 cSide = cross(cDir, cUp);
float targetDepth = 1.0;
vec3 ray = cSide * p.x + cUp * p.y + cDir * targetDepth - cPos;
ray = normalize(ray); // レイを正規化
vec3 groundNormal = vec3(0.0, 1.0, 0.0); // 地面の法線
float groundHeight = 1.0 + (u_mouse.x / u_resolution.x); // マウスのx座標をカメラと地面の距離に対応
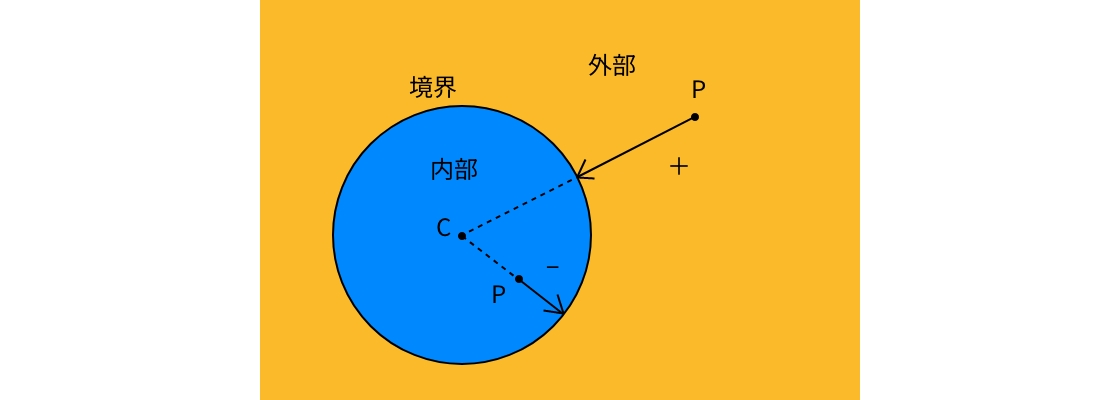
}続いてレイと地面との交点を計算します。交点の位置は、カメラと地面の位置関係と入射角によって計算できます。

入射角はレイが交点に入り込む傾きを表す角度のことです。この入射角 は であるので、の値は 0 以上の値になります。
また、レイ と法線 を長さ 1 に正規化すると、 が得られます。カメラから地面までの高さを とすると、カメラから交点へ向かうベクトルはとなります。これをコードで書くと次のようになります。
// 交点判定
if (dot(ray, groundNormal) < 0.0){
vec3 hit = cPos - ray * groundHeight / dot(ray, groundNormal); // レイと地面の交点
fragColor.rgb = vec3(text(hit.zx)); // 交点のzx座標をテクスチャ座標に対応
} else {
fragColor.rgb = vec3(0.0);
}結果は次のようになります。